何謂選擇排序（Selection Sort）

選擇排序屬於初等排序的其中一種，假設 input 資料共 N 筆存放於 Array[0, 1, ....., (n-1)] 中，則從 index 0 做到 index (n - 2)，共 n - 1 回合，每回合找出 Array[index ~ (n - 1)] 中之最小值，並與 Array[index] 做交換。

Demo

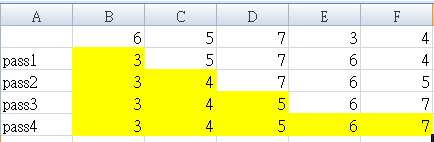
給予：6, 5, 7, 3, 4，(N = 5) 進行 selection sort：

1. index = 0，Array[0 ~ 4] 之最小值為 Array[3]: 3，Array[0] 與 Array[3] 交換。Array = [3, 5, 7, 6, 4]
2. index = 1，Array[1 ~ 4] 之最小值為 Array[4]: 4，Array[1] 與 Array[4] 交換。Array = [3, 4, 7, 6, 5]
3. index = 2，Array[2 ~ 4] 之最小值為 Array[4]: 5，Array[2] 與 Array[4] 交換。Array = [3, 4, 5, 6, 7]
4. index = 3，Array[3 ~ 4] 之最小值為 Array[3]: 6，Array[3] 與 Array[3] 交換。Array = [3, 4, 5, 6, 7]

code

void swap(int arr[], int i, int min){
    int temp = arr[i];
    arr[i] = arr[min];
    arr[min] = temp;
}
void selectionSort(int arr[], int n){
    for(int i = 0; i < n - 1; i++){
        int minIndex = i;
        for(int j = i + 1; j < n; j++){
            if(arr[j] < arr[minIndex]){
                minIndex = j;
            }        
        }
        if(minIndex != i){
            swap(arr, i, minIndex);
        }
    }
}

Time Complexity

Best case: O(n^2)
Worst case: O(n^2)
Average case: O(n^2)
從程式碼來看：無論 input data 是怎樣排列，都須經過 0 ~ (N - 2) 共 (N - 1) 回合的 i 迴圈，每回合 (N - i - 1) 次的 j 迴圈。第一回合做 N - 1 次 j 迴圈，第二回合做 N - 2 次 j 迴圈，到第 (N - 1) 回合做 1 次 j 迴圈。總共：1 + 2 + 3 + ...... + (N - 1) = N(N - 1) / 2 次 = O(N^2)。

Unstable sorting method

假設 input data 為：5(1), 5(2), 2
則排序後：因為 2 為 最小值，5(1) 與 2 對調：2, 5(2), 5(1)
5(1) 出現在 5(2) 之後，因此是 unstable sorting method